2. Le spectrogramme

3. Extension du spectrogramme

4. LPC et ARMA
4.1 Codage LPC
4.2 Modèle AR
4.3 Extension MA
4.4 Modèle ARMA

5. Le cepstre

Le traitement du signal vocal s'inscrit dans une succession de procédures, que ce soit pour la reconnaissance automatique ou pour la synthèse de la parole. Analyse et synthèse sont deux activités duales, l'analyse fournissant une description du signal acoustique que la synthèse utilise pour le reproduire.

Le traitement est aussi utilisé pour réduire la redondance du signal vocal, ou en extraire des paramètres pertinents pour la reconnaissance. Cette réduction par traitement permet aussi de comprimer l'onde avant le stockage ou la transmission.

La reconnaissance a également une activité proche qui est la vérification du locuteur, où on cherche à authentifier une personne grâce à sa voix.

1. Les descriptions temps-fréquences.

Le signal acoustique de la parole est variable dans le temps. Aussi, les descriptions temps-fréquences sont des formes de représentation couramment utilisées en analyse de la parole.

Les termes description, temps et fréquence doivent être pris dans un sens suffisamment large pour inclure diverses formes de représentation et plusieurs notions pour le temps ou la fréquence [ALE 92].

1.1. La fréquence.

La notion de fréquence évoque la répétition dans le temps d’un même motif (par exemple la sinusoïde). On peut distinguer :

avec

‘A’ est l’enveloppe instantanée.

1.2. Le temps.

La notion de temps peut donner lieu à deux interprétations permettant de distinguer:

1.3. La description.

Le signal peut être représenté par une distribution de grandeurs physiques (énergie par exemple) dans le domaine temps-fréquence utilisé, par une décomposition sur une famille de fonction, ou par paramétrisation si on fait référence à un modèle.

^{Retour au début du document}

2. Le spectrogramme.

Le spectrogramme est la représentation temps-fréquence la plus courante. C’est une représentation non paramétrique de la distribution énergétique du signal dans le domaine spectro-temporel.

Le sonagraph est le plus ancien outil utilisé par les phonéticiens pour caractériser la parole. Appareil analogique, il a été supplanté par les calculateurs mettant en oeuvre des algorithmes de TFR [BEL 90] ou de TFD récursive [ROU 93]. Il est ainsi possible, en utilisant des processeurs de signaux, d’obtenir des spectres en temps réel.

Avec l’utilisation des calculateurs, et donc des méthodes numériques, il faut échantillonner et numériser le signal. La fréquence d’échantillonnage est généralement comprise entre 8 et 16 kHz tandis que la quantification se fait sur 8 à 16 bits.

Pour obtenir un spectrographe numérique, on effectue sur le signal une TFR à fenêtre glissante. C’est à dire qu’on analyse une portion limitée du signal, prélevée à l’aide d’une fenêtre de pondération (fenêtre de Hanning par exemple). Pour ne pas perdre d’information et assurer un meilleur suivi des non-stationnarités, les fenêtres se recouvrent. Elles ont généralement une longueur de 256 ou 512 points et le recouvrement est de 50%, soit 128 ou 256 points.

Afin de compenser le niveau plus faible des aigus, il est généralement utilisé un filtre passe-haut, dit de préaccentuation (avec par exemple H(z) = 1 - 0,9z^-1).

Le fondamental (la fréquence de vibration des cordes vocales) produit de nombreux lobes qui perturbent la lecture du spectrogramme, en particulier la position des formants. Afin de s’en affranchir, plusieurs types de lissage sont possibles. Un des plus courant est la pondération de chaque trame spectrale par des fenêtres triangulaires. Ce lissage présente aussi l’avantage de réduire le nombre d’informations, en vue d’une éventuelle reconnaissance sur le spectrogramme. La répartition de ces fenêtres peut être linéaire, ou être faite selon une échelle tenant compte des modèles de perception de l’oreille. On utilise alors une échelle en mel, calculée de la manière suivante :

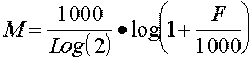avec M en mel et F en Hz [CAL 89].

^{Retour au début du document}

3. Extension de la notion de spectrogramme.

Il est possible d’utiliser d’autres types de distributions ou de décompositions (physiques ou mathématiques) du signal pour obtenir une représentation temps-fréquence [FLA 93] :

Les expressions de ces transformations sont données en annexe G.

Enfin, la référence à un modèle de production ou de perception de la parole permet l’utilisation de représentations paramétriques [DAV 80]. Les paramètres les plus couramment utilisés sont soit des coefficients cepstraux, soit issus d’une modélisation ARMA (ou d’un codage LPC). Les deux paragraphes suivants présentes ces représentations paramétriques du signal de la parole.

^{Retour au début du document}

4. Codage LPC et modélisation ARMA.

4.1. Principes du codage LPC.

Le codage par prédiction linéaire, ou LPC (Linear Predictive Coding) repose sur la connaissance du modèle de production de la parole tel qu’il est décrit par la figure 1 du paragraphe 1.3. Ce modèle peut être décomposé en deux parties : la source, active, et le conduit, passif.

Pour les sons non voisés, le signal d’excitation est un bruit blanc de moyenne nulle et de variance unité. Pour les sons voisés, cette excitation est une suite d’impulsions d’amplitude unité :

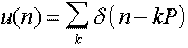
où P est la période du fondamental (Pitch period).

Le codage LPC consiste à estimer le modèle décrivant le conduit, en connaissant le signal excitation.

4.2.Modèle AR.

En fait, les deux excitations utilisées pour le codage LPC sont idéalisées, car la forme réelle de l’impulsion glottale et celle du rayonnement aux lèvres sont comprises dans l’expression de la transmittance du modèle. En première approximation, cette transmittance est celle d’un filtre polynomial, de la forme 1/A(z) et elle est excitée par les signaux d’excitations décrits.

Le polynôme A(z) est noté :

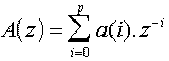avec a(0)=1.

Ce modèle de production d’un signal est appelé autorégressif (AR), récursif, tous-pôles, ou encore IIR (Infinite Impulse Response). Le signal ainsi produit à pour transformée en Z :

Y(z) = U(z) / A(z)

Dans le domaine temporel, on peut écrire l’équation récurrente suivante:

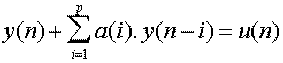(1)

Cette récurrence exprime le fait qu’un échantillon quelconque y(n) peut être déterminé par une combinaison linéaire des échantillons qui le précèdent, ajoutée au terme d ’excitation. Les coefficients a(i) sont dit prédicteurs.

Si le signal d ’excitation n’est pas accessible, la quantité :

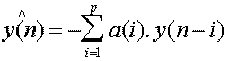(2)

est la prédiction de y(n) conditionnellement à son passé. En rapprochant (1) et (2), on peut interpréter u(n) comme étant une erreur de prédiction :

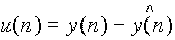
Si, de plus, on cherche à estimer le modèle par observation du signal, cela justifie la recherche des coefficients a(i) optimaux, en minimisant cette erreur de prédiction, ou plutôt sa variance s² dans le cas d'un bruit blanc. On parle alors de prédiction linéaire.

4.3. Extension MA du modèle.

La modélisation AR du mécanisme de la phonation présente des limitations et ne caractérise que d’une manière approchée la production de la parole, en particulier pour les sons nasalisés. Le modèle du conduit nasal est en réalité un filtre pôles-zéros (ARMA: autorégressif à moyenne ajustée ou Auto-Regressive Moving Average) et celui du rayonnement aux lèvres est du type tous-zéros (MA: moyenne ajustée ou encore FIR: Finite Impulse Response).

La transmittance devient alors celle d’un modèle ARMA :

D(A, B) = g(I, J) / (I + J)

où A(z) est la partie AR et B(z) représente la partie MA.

Cela donne dans le domaine temporel la récurrence suivante :

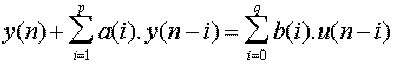
Chaque échantillon y(n) est la combinaison linéaire de p échantillons passés et de q+1 échantillons présents et passés de l’excitation.

4.4. Conclusion sur la modélisation ARMA.

Si le modèle ARMA est souvent retenu pour modéliser la parole suivant le principe généralement retenu (figure 1, paragraphe 1.3), il n’est pas exempt de limitations.

Le modèle ARMA est plus délicat à estimer qu’un modèle AR. Cela amène parfois à préférer, pour une qualité donnée de la modélisation, un modèle AR avec un ordre un peu surestimé.

Mais la principale limitation réside dans l’hypothèse de stationnarité du signal acoustique qui est faite. Il faut réaliser un compromis entre la longueur de la fenêtre d’analyse et la durée pendant laquelle l’hypothèse de stationnarité est raisonnable. Ce compromis est réalisable pendant les zones stables (voyelles), mais il n’est pas satisfaisant durant les phases transitoires et injustifié sur les plosives.

Plusieurs méthodes d’estimations des modèles ARMA sont décrites dans la littérature [CAL 89] ou [BOI 87] : méthode de corrélation (algorithmes de Levinson ou de Schur), de covariance (algorithme de Cholesky), de Burg.

^{Retour au début du document}

5. Le cepstre.

Contrairement au spectrogramme qui ne fait appel à aucune connaissance a priori sur le signal acoustique, le cepstre est basé sur une connaissance du mécanisme de production de la parole. On part de l’hypothèse que la suite s_n constituant le signal vocal est le résultat de la convolution du signal de la source par le filtre correspondant au conduit :

s_n = u_n * b_n avec s_n le signal temporel, u_n le signal excitateur, b_n la contribution du conduit.

Le but du cepstre est de séparer ces deux contributions par déconvolution. Il est fait l’hypothèse que g_n est soit une séquence d’impulsions (périodiques, de période T₀, pour les sons voisés), soit un bruit blanc, conformément au modèle de production. Une transformation en Z permet de transformer la convolution en produit :

S(z) = U(z) . B(z)

Le logarithme (du module uniquement car on ne s’intéresse pas à l’information de phase) transforme le produit en somme. On obtient alors:

Log |S(z)| = Log |U(z)| + Log |B(z)|

Par transformation inverse, on obtient le cepstre. Dans la pratique, la transformation en Z est remplacée par une TFR. L’expression du cepstre est donc :

ç(n) = FFT ^-1(Log(FFT(s(n))))

L'espace de représentation du cepstre (espace quéfrentiel) est homogène au temps et il est possible, par un filtrage temporel (liftrage), de séparer dans le signal, la contribution de la source de celle du conduit. Les premiers coefficients cepstraux contiennent l’information relative au conduit. Cette contribution devient négligeable à partir d’un échantillon n₀. Les pics périodiques visibles au-delà de n₀, reflètent les impulsions de la source.

A partir du cepstre, il est possible de définir la fréquence fondamentale de la source g_n en détectant les pics périodiques au-delà de n₀. Le spectre du cepstre pour les indices inférieurs à n₀ permettra d’obtenir un spectre lissé, débarrassé des lobes dus à la contribution de la source.

^{Retour au début du document}