2 Distributions

3 Produit de convolution
3.1 Présentation
3.2 Calcul
3.3 Propriétés
3.4 Exercice

1. Intégration

1.1 Intégrale.

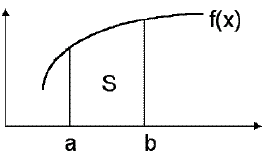
Une intégrale est un nombre, représentant une aire (surface) généralement délimitée par l'axe des abscisses, deux valeurs (éventuellement infinies) sur cet axe et la courbe d'une fonction y=f(x).

1.2 Primitive.

La primitive F(x) d'une fonction f(x) est telle que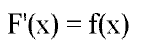, c'est à dire que sa dérivée est f(x). Elle permet de calculer la surface S de la figure précédente:

^{Retour au début du document}

2 Distributions.

Certains des outils qu'on va voir par la suite s'appliquent non pas à des fonctions, mais à des distributions. En fait cette "nuance" ne nous gênera pas trop, peu de chose étant "démontré mathématiquement".

3 Le produit de convolution.

3.1 Présentation.

Soit deux fonctions e(t) et h(t), le produit de convolution est l’opération :

C’est une moyenne de h pondérée par e.

Physiquement, h est l’influence de l’instrument de mesure sur l’observation de e.

Le filtrage d’un signal et l'observation d'un signal au travers un appareil de mesure quelconque (car cette observation est un filtrage …) sont des produits de convolution. Donc, on observe pas e(t), mais s(t).

3.2 Calcul.

On a une intégration sur R, donc de -inf à +inf. Un signal, ici e(t), subit un "miroir horizontal" et se "promène" devant l'autre. On mesure en permanence la surface (l'intégrale ...) commune sous les deux courbes.

Par exemple pour deux signaux h(t) et e(t):

Le signal convolué h*e se construit:

3.3 Propriétés.

Parmi les propriétés du produit de convolution, notons la commutativité: h*e = e*h. Cela tombe bien, car on peut ainsi "promener" celui des deux signaux qui nous arrange le plus (utile lorsqu'un des deux n'est pas borné ...).

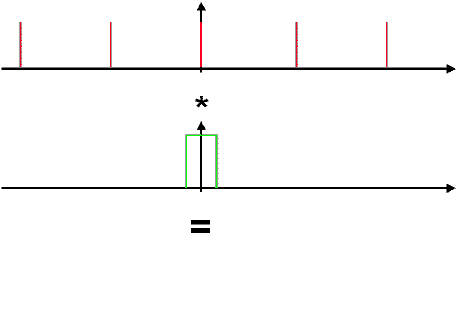
L'impulsion de Dirac est l'élément neutre de la convolution: e*d = e.

3.4 Exercice d'exemple.

^{Retour au début du document}