Transformée de Fourier

1 Spectre

2 Propriétés de la TF
2.1 Réversibilité
2.2 Linéarité
2.3 Changement d'échelle
2.4 Théorème du retard
2.5 Modulation
2.6 Théorème de Plancherel

1. Spectre.

L’opérateur qui permet de calculer le spectre d’un signal continu est la transformée de Fourier :

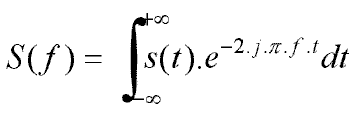
^{^{Retour
au début du document}}

2. Propriétés de la TF

2.1 Réversibilité.

Cet opérateur est réversible, permettant à partir du spectre de retrouver le signal temporel :

Cette propriété peut s'avérer bien pratique pour effectuer un filtrage complexe:

	passage dans le domaine spectral,
	modification du spectre
	retour dans le domaine temporel

ou pour générer un signal complexe:

	description dans le domaine spectral,
	passage dans le domaine temporel. ^{^{Retour au début du document}}

2.2 Linéarité.

Si un signal x(t) est une combinaison linéaire de signaux s_i(t), le spectre X(f) est un combinaison linéaire des spectres S_i(f) :

2.3 Changement d’échelle.

Plus un signal "est large", plus son spectre "est étroit".

A la limite, lorsque a tend vers ¥, 1/a tend vers 0 et le spectre tend donc vers une impulsion de Dirac.

De même, si on considère des portes de plus en plus étroites (a/2, a/4, …) mais de plus en plus haute (2/a, 4/a, …), afin de leur conserver une surface constante égale à 1, les spectres deviennent des sinus cardinaux de plus en plus larges. A la limite, lorsque la porte tend vers une impulsion de Dirac, le spectre tend vers une valeur constante égale à 1.

d (t) ß T.F. à 1

1 ß T.F. à d (f)

^{^{Retour
au début du document}}

s(t).x(t) ß T.F. à S(f)*X(f)

^{^{Retour
au début du document}}

1. Spectre.

2. Propriétés de la TF

2.1 Réversibilité.

2.2 Linéarité.

2.3 Changement d’échelle.

2.4 Théorème du retard.

2.5 Modulation.

2.6 Théorème de Plancherel.