|
Un ordinateur est un système numérique et ne sait
donc manipuler que des nombres. Pour le faire travailler sur un signal réel
continu, il faut numériser le signal. La numérisation est une
succession de trois étapes.
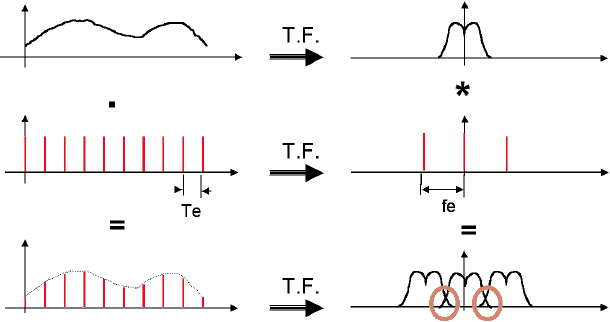
L’échantillonnage consiste à représenter un signal s(t) par la
suite de ses valeurs s(nT) à des instants multiples entiers d’une durée
T, la période d’échantillonnage.
Cela revient à multiplier s(t) par CT un
peigne de Dirac de période T.
Une multiplication en temporel correspond à une convolution en fréquentiel.
Le spectre est donc périodique, de période fe=1/T.
On s‘aperçoit que si fe < 2fsmax, les
spectres se chevauchent (repliement de spectre).
Le théorème de Shannon nous dit que fe ³
2fsmax.
Il y a deux possibilités d'appliquer Shannon:
 | Si fsmax est connu et dans des limites
technologiquement acceptables, on choisit fe en conséquence. |
| Si fsmax est indéterminée (ou infinie ...), on fixe fe
(il est quand même nécessaire d'avoir un minimum de connaissance
du signal ...) et on applique sur le signal un filtre passe bas éliminant
les fréquences > 2fe. On a alors un erreur, mais on
le sait. On tiendra compte du fait qu'un filtre n'est pas parfait
autour de sa fréquence de coupure... |
Une propriété intéressante du spectre :
| Signal périodique Û
spectre échantillonné. |
| Signal échantillonné Û
spectre périodique. |
 Retour
au début du document
L’opération suivante est la quantification. Elle
est l’approximation de chaque valeur du signal s(t) ou s(nT) par un
entier multiple d’une quantité élémentaire q, échelon de
quantification.
Cette opération entraîne une erreur dans la mesure du
signal s(t) (sq(1,2)=1 et sq(1,7)=1 par exemple).
Cette erreur est inférieure à |q| et amène un bruit de
quantification.
La
représentation binaire des éléments de quantification est le codage.
Il peut se faire de plusieurs manières : directe, par complément
à 1 ou à 2, signe et valeur absolue, etc.
Retour
au début du document
Une chaîne de numérisation à donc généralement l’allure suivante :
Ce
principe se retrouve aussi bien dans une carte son, que dans une carte
d’acquisition vidéo ou une carte d’entrées/sorties analogique.
Une variation sur le même thème permettait (je ne
pense pas qu'elle soit encore très courante) d'avoir un meilleure
précision:
Le résultat de la conversion s(nT) est converti en
signal analogique et comparé au signal original. On a donc une image de
l'erreur de conversion. Celle-ci est à son tour numérisé.
Retour
au début du document
|
