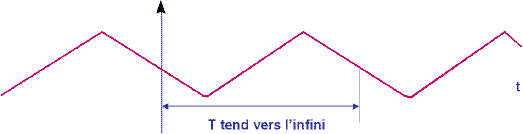
Un signal quelconque peut être considéré comme la limite d’un
signal périodique dont la période devient infiniment longue : les
motifs s’éloignent les uns des autres, si bien qu’il ne reste plus
qu’un seul motif dans l’espace d’observation.
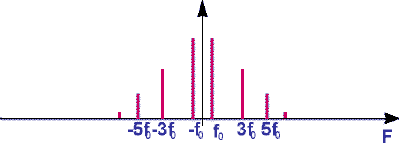
Si on accepte cette considération, dans le domaine fréquentiel, la
fréquence du fondamental f0 tend vers 0 (selon le principe
vu ici). Les harmoniques étant
des multiples du fondamental, ceux-ci se rapprochent et "finissent
par se toucher". Le spectre n’est alors plus un spectre discret
(de raie), mais un spectre continu.
La
série de Fourier (somme discrète) «tend» vers une somme continue, la
transformée de Fourier.
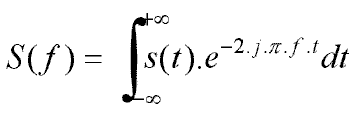
Par exemple, un signal « porte » de
largeur t à pour spectre un sinus cardinal:
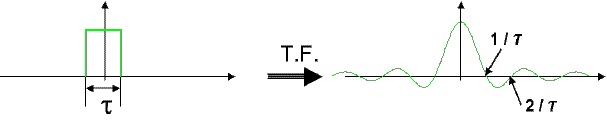
ou encore le peigne de Dirac qui a pour TF ... un peigne
de Dirac:
Retour
au début du document